සන්නිකර්ෂණය මගින් වර්ගමූලය සෙවීම.

සෑම සංඛ්‍යාවකම වර්ගයක් ඇති බව පැහැදිලි ය. නමුත් සෑම සංඛ්‍යාවකම වර්ගමූලයක් තිබේද? ඒ පිළිබඳ ව දැන් විමසා බලමු.
ඉහත වගුව අනුව, 4 හි වර්ගමූලය 2 වන අතර, 9 හි වර්ගමූලය 3 වේ. 4ත් 9ත් අතර ඇති සංඛ්‍යාවල වර්ගමූල වන්නේ 2ත් 3ත් අතර ඇති අගයන් ය. ඒ අනුව, 4ත් 9ත් අතර ඇති සංඛ්‍යාවල වර්ගමූල නිඛිල නොවන බව පැහැදිලි ය. ඒවා දශම සංඛ්‍යා වේ. එම වර්ගමූල ආසන්න ලෙස සොයන අයුරු මෙම පාඩමේ දී සලකා බැලේ. එවැනි ආසන්න අගයකට සන්නිකර්ෂණයක් යැයි කියනු ලැබේ.
නිදසුනක් ලෙස, 5හි වර්ගමූලය සඳහා සන්නිකර්ෂණයක් සොයන අයුරු සලකා බලමු.
පහත දැක්වෙන වගුව බලන්න.

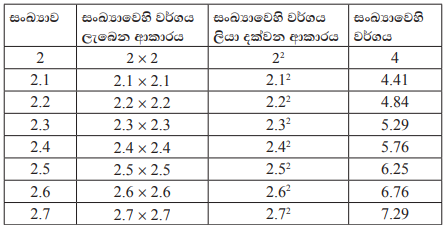
ඉහත වගුවෙහි දකුණු පස කෙලවර තීරුවේ ඇති අගය අතුරින් 5ට ආසන්නම අගය දෙක වන්නේ 4.84 හා 5.29යි. ඒවා පිළිවෙළින් 2.2හි හා 2.3හි වර්ගයයි.
වගුව අනුව, 4.84හි හා 5.29හි වර්ගමූල පිළිවෙළින් 2.2 හා 2.3 වේ. සංකේතාත්මක ව, √4.84=2.2 ද √5.29=2.3 ලෙස ලිවිය හැකි ය.
දැන්, 5ට වඩා ආසන්න අගය වන්නේ 4.84 ද, එසේ නැතිනම් 5.29 දැයි පරීක්ෂා කරමු.
4.84ත් 5ත් අතර වෙනස = 5 − 4.84 = 0.16
5.29ත් 5ත් අතර වෙනස = 5.29 − 5 = 0.29
ඒ අනුව, 5ට වඩාත් ආසන්න අගය 4.84යි. එමනිසා, 5හි වර්ගමූලය සඳහා ආසන්න අගයක් ලෙස 2.2 ගත හැකි ය. මෙසේ, යම් ධන නිඛිලයක වර්ගමූලය සඳහා දශමස්ථාන එකකට නිවැරදි ව ලැබෙන අගයට එම සංඛ්‍යාවේ වර්ගමූලයේ “පළමු දශමස්ථානයට
සන්නිකර්ෂණය” (හෝ, වඩාත් සරල ව, “පළමු සන්නිකර්ෂණය”) යැයි කියනු ලැබේ.
මේ අනුව, 5හි වර්ගමූලය සඳහා පළමු සන්නිකර්ෂණය 2.2 වේ. ආසන්න අගය දැක්වීමේ දී සංකේතය යොදා ගැනේ. ඒ අනුව, √5≈2.2ලෙස ද ලියා දැක්විය හැකි ය.
මේ ආකාරයෙන් ම හේතු දක්වමින්, ඉහත වගුව අනුසාරයෙන්, 6හි වර්ගමූලයේ පළමු සන්නිකර්ෂණය 2.4 බවත්, 7හි වර්ගමූලයේ පළමු සන්නිකර්ෂණය 2.6 බවත් නිගමනය කළ හැකි ය. එනම්,
√6≈2.4
√7≈2.6
යම් පූර්ණ වර්ගයක් නොවන ධන සංඛ්‍යාවක වර්ගමූලය සඳහා පළමු සන්නිකර්ෂණයක් සොයන නිශ්චිත ක්‍රමයක් පහත නිදසුන් මගින් උගෙන ගනිමු.

නිදසුන 1
√17 සඳහා පළමු දශමස්ථානයට සන්නිකර්ෂණය සොයන්න.
මුලින්ම 17 ඇත්තේ කුමන පූර්ණ වර්ග දෙක අතර දැයි සොයා ගත යුතු ය.
● 17 ට අඩු පූර්ණ වර්ග සංඛ්‍යා අතුරින් 17ට ආසන්නම පූර්ණ වර්ගය 16 වන අතර, 17ට වැඩි පූර්ණ වර්ග සංඛ්‍යා අතුරින් 17ට ආසන්නම පූර්ණ වර්ගය 25 වේ.
ඒ අනුව, 16 < 17 < 25 ලෙස ලියමු.
● එම එක් එක් සංඛ්‍යාවල වර්ගමූලය ලියූ විට
√16 < √17 < √25
∴ 4 < √17 < 5
ඒ අනුව 17 හි වර්ගමූලය, 4ත් 5ත් අතර පිහිටයි.
එනම්, √17 හි අගය 4ත් 5ත් අතර වේ.
● 17 වඩා ආසන්න වන්නේ 16ට ද 25ට ද සොයා ගනිමු.
16ත් 17ත් අතර වෙනස 1 කි.
17ත් 25ත් අතර වෙනස 8 කි.
∴ 17 වඩා ආසන්න වන්නේ 16ට ය.
∴ √17 හි අගය 5ට වඩා 4ට ආසන්න අගයක් වේ.
එමනිසා 4.1, 4.2, 4.3 හා 4.4 සංඛ්‍යා අතරින් එක් සංඛ්‍යාවක් √17 හි පළමු සන්නිකර්ෂණය වේ.
මේවා අතුරින් √17 ට ආසන්නම අගය සෙවීමට එක් එක් සංඛ්‍යාව වර්ග කරමු. මුල් සංඛ්‍යා දෙක වර්ග කළ විට
4.14 x 4.1 = 16.81
4.2 x 4.2 = 17.64
ලැබේ. 4.2² හි අගය 17 ඉක්මවා යන හෙයින් 4.3² හා 4.4² සෙවීම අනවශ්‍ය වේ.
තව ද, 16.81 හා 17.64 සංඛ්‍යා අතුරින් 17 වඩා ආසන්න අගය 16.81 නිසා √17 හි පළමු සන්නිකර්ෂණය 4.1 වේ.

නිදසුන 2
√245 හි පළමු සන්නිකර්ෂණය සොයන්න.
15² = 225 ද 16² = 256 ද බැවින්
225 < 245 < 256 ලෙස ලියාගන්න.
ඒ අනුව, 15 < √245 < 16
∴ √245 හි අගය 15ත් 16ත් අතර වේ.
245 වඩාත් ආසන්න වන්නේ 256ට බැවින් √245 හි අගය 15ට වඩා 16ට ආසන්න වේ.
එනම්, එය 15.5, 15.6, 15.7, 15.8, 15.9 යන අගයන්ගෙන් එකකි. එම අගය නිර්ණය කරමු.
15.9 x 15.9 = 252.81
15.8 x 15.8 = 249.64
15.7 x 15.7 = 246.49
15.6 x 15.6 = 243.36
ඉහත අගය අතරින් 245ට වඩාත් ම ආසන්න අගය 246.49 වේ.
∴ √245 හි පළමු සන්නිකර්ෂණය 15.7 වේ.