සාධක හඳුනා ගැනීම
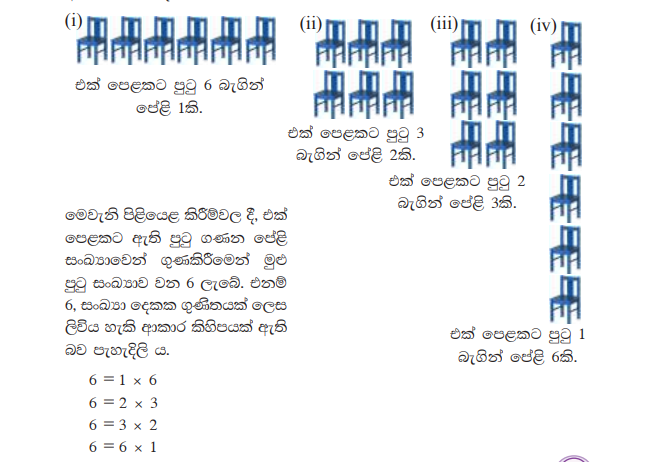
සිසුන් හය දෙනකු සිටින පන්තියක් සලකන්න, සෑම පේළියක ම සමාන සිසුන් සංඛ්යාවක් අසුන් ගත යුතු ය. ඒ සඳහා පුටු 6ක් පිළියෙළ කළ හැකි ආකාර පහත දැක්වේ.
සෑම පේළියක ම සමාන පුටු ගණනක් ලැබෙන සේ පුටු 12ක් පිළියෙල කළ හැකි ආකාර සියල්ල සලකමු. මෙම එක් එක් පිළියෙල කිරීම්වල දී එක් පෙළකට ඇති පුටු ගණන, පේළි සංඛ්යාවෙන් ගුණ කිරීමෙන්, මුළු පුටු ගණන වන 12 ලැබේ. එනම් 12 සංඛ්යා දෙකක ග-ණිතයක් ලෙස ලිවිය හැකි ආකාර කිහිපයක් ඇති බව පැහැදිලි වේ.
12= 1 × 12
12= 2 × 6
12= 3 × 4
12= 4 × 3
12= 6 × 2
12= 12 × 1
මෙලෙස ඕනෑ ම පූර්ණ සංඛ්යාවක්, පූර්ණ සංඛ්යා දෙකක ගුණිතයක් ලෙස ලිවිය හැකි ය.
කිසියම් පූර්ණ සංඛ්යාවක්, පූර්ණ සංඛ්යා දෙකක ගුණිතයක් ලෙස ලියූ විට, ඒවා එක එකක් මුල් සංඛ්යාවේ සාධක ලෙස හැඳින්වේ.
6 = 1 × 6 බැවින්, 1 සහ 6, 6හි සාධක වේ.
6 = 2 × 3 බැවින්, 2 සහ 3, 6හි සාධක වේ.
6ට අදාළ ගුණිතයන් සලකා බැලූ විට, 6හි සාධක 1, 2, 3 සහ 6 වේ. එලෙස ම, 12හි සාධක 1, 2, 3, 4, 6 සහ 12 වේ.
දැන්, අපි 16හි සාධක සොයමු.
පහත පරිදි 16, පූර්ණ සංඛ්යා දෙකක ගුණිතයක් ලෙස ලිවිය හැකි ආකාර සියල්ල සලකා බලමු.
16 = 1 × 16
16 = 2 × 8
16 = 4 × 4
16 = 8 × 2
16 = 16 × 1
ඒ අනුව 16හි සාධක 1, 2, 4, 8 සහ 16 වේ.
ඉහත 16ට අදාළ ගුණිතයන් සලකා බැලූ විට, 16හි සාධක ලබා ගැනීමට පහත ගුණිතයන් පමණක් ලිවීම ප්රමාණවත් බව පෙනෙයි.
16 = 1 x 16
16 = 2 x 8
16 = 4 x 4