ස්ථානීය අගය
![]() සංඛ්යා ලිවීමේ දී, අප බහුල ව භාවිත කරන්නේ හින්දු අරාබි සංඛ්යා ක්රමය යි.
සංඛ්යා ලිවීමේ දී, අප බහුල ව භාවිත කරන්නේ හින්දු අරාබි සංඛ්යා ක්රමය යි. ![]() එම ක්රමය අනුව සංඛ්යා ලිවීමේ දී 0, 1, 2, 3, 4, 5, 6, 7, 8 හා 9 යන ඉලක්කම් දහය භාවිත කරනු ලැබේ.
එම ක්රමය අනුව සංඛ්යා ලිවීමේ දී 0, 1, 2, 3, 4, 5, 6, 7, 8 හා 9 යන ඉලක්කම් දහය භාවිත කරනු ලැබේ.![]() බින්දුවේ සිට නවය තෙක් ඇති සංඛ්යාවක් ලිවීමේ දී, අප එක් ඉලක්කමක් එක් ස්ථානයක ලියයි.
බින්දුවේ සිට නවය තෙක් ඇති සංඛ්යාවක් ලිවීමේ දී, අප එක් ඉලක්කමක් එක් ස්ථානයක ලියයි.![]() උදාහරණයක් ලෙස, තුන යන සංඛ්යාව ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 3 ලෙස ය.
උදාහරණයක් ලෙස, තුන යන සංඛ්යාව ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 3 ලෙස ය. ![]() එනම්, 3 ලිවීමට එක් ස්ථානයක් භාවිත කරනු ලැබේ.
එනම්, 3 ලිවීමට එක් ස්ථානයක් භාවිත කරනු ලැබේ. ![]() එක් ස්ථානයක් පමණක් යොදා ගෙන ලිවිය හැකි විශාලතම සංඛ්යාව 9 වේ.
එක් ස්ථානයක් පමණක් යොදා ගෙන ලිවිය හැකි විශාලතම සංඛ්යාව 9 වේ.![]() නවයට වඩා එකකින් විශාල සංඛ්යාව දහය වේ.
නවයට වඩා එකකින් විශාල සංඛ්යාව දහය වේ. ![]() දහයේ සිට අනූ නවය තෙක් ඇති සංඛ්යාවක් ලියන්නේ, ඉලක්කම් දෙකක් හෝ එක ම ඉලක්කම දෙවතාවක් හෝ ස්ථාන දෙකක් යොදා ගෙන ලිවීමෙනි.
දහයේ සිට අනූ නවය තෙක් ඇති සංඛ්යාවක් ලියන්නේ, ඉලක්කම් දෙකක් හෝ එක ම ඉලක්කම දෙවතාවක් හෝ ස්ථාන දෙකක් යොදා ගෙන ලිවීමෙනි.![]() උදාහරණයක් ලෙස, දහය යන සංඛ්යාව, ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 10 ලෙස ය.
උදාහරණයක් ලෙස, දහය යන සංඛ්යාව, ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 10 ලෙස ය. ![]() අනූ නවය යන සංඛ්යාව, ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 99 ලෙස ය.
අනූ නවය යන සංඛ්යාව, ඉලක්කම් භාවිත කර ලියනු ලබන්නේ 99 ලෙස ය. ![]() එනම්, 10 සහ 99 ලිවීමට ස්ථාන දෙක බැගින් භාවිත කරනු ලැබේ.
එනම්, 10 සහ 99 ලිවීමට ස්ථාන දෙක බැගින් භාවිත කරනු ලැබේ.![]() දැන් අපි 3 හා 5 යන ඉලක්කම් දෙක, ස්ථාන දෙකක යොදමින් ලියන සංඛ්යා කිහිපයක් විමසා බලමු.
දැන් අපි 3 හා 5 යන ඉලක්කම් දෙක, ස්ථාන දෙකක යොදමින් ලියන සංඛ්යා කිහිපයක් විමසා බලමු.![]() 3 හා 5 යන ඉලක්කම් දෙක 35 ලෙස ලියූ විට සංඛ්යාව “තිස් පහ” වේ.
3 හා 5 යන ඉලක්කම් දෙක 35 ලෙස ලියූ විට සංඛ්යාව “තිස් පහ” වේ.![]() 3 හා 5 යන ඉලක්කම් දෙක 53 ලෙස ලියූ විට සංඛ්යාව “පනස් තුන” වේ.
3 හා 5 යන ඉලක්කම් දෙක 53 ලෙස ලියූ විට සංඛ්යාව “පනස් තුන” වේ.![]() එනම් 3 හා 5 යන එක් එක් ඉලක්කම පිහිටන ස්ථානය අනුව ලැබෙන සංඛ්යා එකිනෙකට වෙනස් වේ.
එනම් 3 හා 5 යන එක් එක් ඉලක්කම පිහිටන ස්ථානය අනුව ලැබෙන සංඛ්යා එකිනෙකට වෙනස් වේ.![]() දැන් අපි සංඛ්යාවක, එක් එක් ඉලක්කම පිහිටන ස්ථානයට අදාළ ස්ථානීය අගයත්, එක් එක් ඉලක්කමෙන් නිරූපිත අගයත් පැහැදිලි කර ගනිමු.
දැන් අපි සංඛ්යාවක, එක් එක් ඉලක්කම පිහිටන ස්ථානයට අදාළ ස්ථානීය අගයත්, එක් එක් ඉලක්කමෙන් නිරූපිත අගයත් පැහැදිලි කර ගනිමු.
● පබළු තිස් පහක් ගෙන දහය බැගින් වැල්වලට ඇමුණූ විට දහයේ පබළු වැල් 3ක් ලැබෙන අතර, පබළු 5ක් ඉතිරි වේ.
![]() පබළු තිස් පහ, දහයේ ඒවා තුනකටත්, එකේ ඒවා පහකටත් වෙන් කළ හැකි ය.
පබළු තිස් පහ, දහයේ ඒවා තුනකටත්, එකේ ඒවා පහකටත් වෙන් කළ හැකි ය.
එනම්,
තිස් පහ = දහයේ ඒවා 3 + එකේ ඒවා 5 = 35
![]() ඉහත පැහැදිලි කිරීමට අනුව, තිස්පහෙහි එකේ ඒවා 5 නිරූපණය කිරීමට, 5 ඉලක්කම ලියන ස්ථානයෙහි ස්ථානීය අගය 1 ලෙස ගෙන ඇත.
ඉහත පැහැදිලි කිරීමට අනුව, තිස්පහෙහි එකේ ඒවා 5 නිරූපණය කිරීමට, 5 ඉලක්කම ලියන ස්ථානයෙහි ස්ථානීය අගය 1 ලෙස ගෙන ඇත. ![]() එම ස්ථානය එකස්ථානය ලෙස නම් කරනු ලැබේ.
එම ස්ථානය එකස්ථානය ලෙස නම් කරනු ලැබේ.![]() තිස් පහෙහි, දහයේ ඒවා 3 නිරූපණය කිරීමට එකස්ථානයට වම් පසින් වූ ස්ථානයෙහි ස්ථානීය අගය 10 ලෙස ගෙන, 3 ඉලක්කම එම ස්ථානයෙහි ලියා ඇත.
තිස් පහෙහි, දහයේ ඒවා 3 නිරූපණය කිරීමට එකස්ථානයට වම් පසින් වූ ස්ථානයෙහි ස්ථානීය අගය 10 ලෙස ගෙන, 3 ඉලක්කම එම ස්ථානයෙහි ලියා ඇත. ![]() එම ස්ථානය දසස්ථානය ලෙස නම් කරනු ලැබේ.
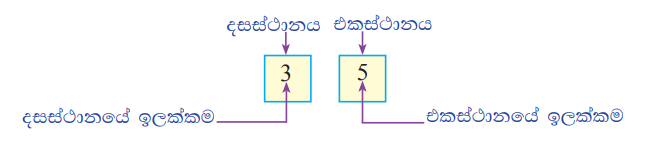
එම ස්ථානය දසස්ථානය ලෙස නම් කරනු ලැබේ.![]() එක් එක් ස්ථානය හතරැස් කොටුවකින් සලකුණු කොට, 35හි එක් එක් ඉලක්කමේ පිහිටීම පහත රූපයේ දක්වා ඇත.
එක් එක් ස්ථානය හතරැස් කොටුවකින් සලකුණු කොට, 35හි එක් එක් ඉලක්කමේ පිහිටීම පහත රූපයේ දක්වා ඇත.